Creating an arbitrary/custom distribution for constraints for constrained random testing
Top of this page The problem to be solved The distribution The code Testing Problems TODO
Other projects

So there you are working diligently away doing your ASIC Verification Engineer thing and writing complicated constraints and there are no cases of corners out of your reach and your boss says, "OK smartypants, let's see you make a random distribution like this," and then your boss scribbles some arbitrary curve that does not look readily amenable to a simple mathematical expression.

So what do you do?

This page offers a suggestion.

It is also up on EDA Playground here:      

The problem to be solved

SystemVerilog provides several distributions one can use out of the box. They are:

• $random • $dist_chi_square • $dist_erlang
• $dist_exponential • $dist_normal • $dist_poisson
• $dist_t • $dist_uniform • expression dist { dist_list } ;
because you can dist across a list.

What it does not have is a handy distribution for a scribble, like the one in this video and shown in a still on the right:

         


What I would like to do is this: 
  ...
  int theData ;
  ...
  theData = dist_arbitrary (MinValue, MaxValue) ;
  ...
I myself can think of many reasons why someone would want a custom distribution, but the most interesting one
is that I have not seen someone else do it yet. So here's a solution using the DPI. The actual function call in the
SystemVerilog side is shown below. The first time through the pre_randomize function uses a DPI-C call to set up
the distribution, and subsequent calls just get a value from that distribution: 

class box_t;
  static int firsttime = 1 ;
  int theData;
  //             ------  NOT A COMMENT TO IGNORE  -------
  //  The constraint below is what I'd like to mimic, but SystemVerilog
  //  does not have an arbitrary distribution function. So I made one.
  //  constraint  the_index 
  //  { 
  //    theData = $dist_arbitrary (`X_MINVAL, `X_MAXVAL);
  //  }
  //  Note that the variable 'theData' is NOT rand, because all the work
  //  happens on the C-side in pre-randomize and we can't have 'theData'
  //  being scrambled after its holiday visit to the C-side.


  function void pre_randomize();
    if (firsttime == 1)
    begin
      firsttime = 0 ;
      theData = dist_arb(0, `X_MINVAL, `X_MAXVAL) ; // theData here is tossed
    end
      theData = dist_arb(1, `X_MINVAL, `X_MAXVAL) ;
  endfunction : pre_randomize
endclass : box_t


The distribution

One has to capture the curve somehow. I used gimp on both a 1024x400 and a 1024x256 canvas.

As long as you maintain a continuous line monotonic in X, it lends itself to trivial scripting.

I exported the scribble to html ... because, reasons. That html file is huge, but if you are curious it's here:Untitled.html.txt.

A small perl script converted it into a single list of Y values in a file X lines long (1024).

So that's : 
% more htmlFromPngToCSV.pl

#!/usr/bin/perl

$rowcount = 0 ;
$colcount = 0 ;

while (<STDIN>)
{
  if ($_ =~ /\<TR\>/)
  {
    $rowcount++ ;
    $colcount = 0 ;
  }
  elsif ($_ =~ /BGCOLOR(.*?)/)
  {
    if ($_ =~ /.*?#\d+/)
    {
      $PLOT[$colcount] = $rowcount ;
    }
    $colcount++ ;
  }
}
$ymax = $rowcount ;

foreach $col (@PLOT)
{
  $inverted = $ymax - $PLOT[$col] ;
  print ("$inverted\n") ;
}

% cat Untitled.html | ./htmlFromPngToCSV.pl > arbitrary_distribution_file.txt
I gave that to gnuplot just to check the translation: 
% more a.dat 
set terminal png ; 
set output "test.png" ; 
plot "arbitrary_distribution_file.txt" w lines lc 3 ; 
set terminal x11 ; 
replot
% gnuplot -background white -persist a.dat



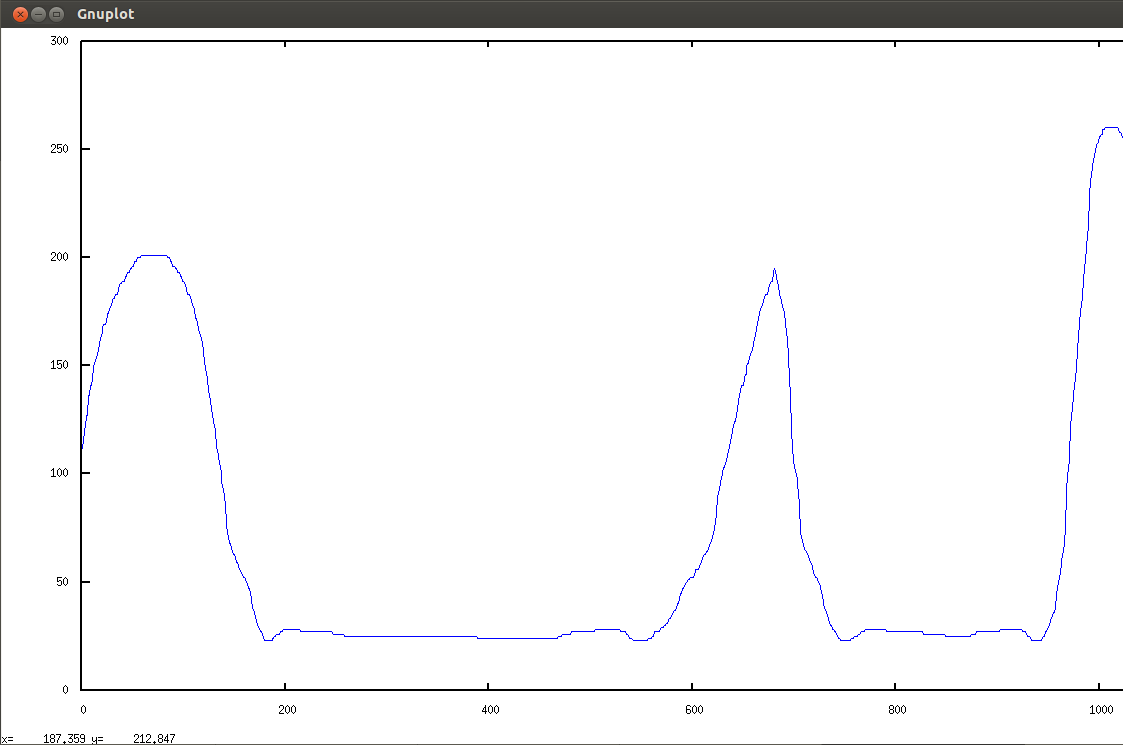
I now have a text file I can read into the SystemVerilog simulation.
Recall that what we need is to be able to do something that functions like this from the SystemVerilog side: 
  theData = dist_arbitrary (MinValue, MaxValue) ;

There are two conversions that must happen. The first is to turn that X-Y plot into a probability distribution, and the
second is to fit return values into the requested MinValue to MaxValue range. The program dist_arb.c performs both
functions and is provided with explanatory notes further below.


Conversion 1: Making the probability distribution
This comes straight out of a box, in this case a genetic algorithm box. There is a GA description here
A Genetic Algorithm Demo project,
but the basic idea is to create what is called a Weighted Wheel, which is an array containing
Y0@X0 values of X0,
Y1@X1 of X1,
... Yn@Xn of Xn.
For a distribution of three values, 1, 2, and 3, which has 20% probability of 1,
50% probability of 2, and 30% probablilty of 3, the array looks like this:
               1111111111 // 10
2222222222222222222222222 // 25
          333333333333333 // 15
or
11111111112222222222222222222222222333333333333333

Chosing any index into the array gets a return value in the ratios shown above.


Conversion 2: Fitting the distribution into a min - max range
Whatever one wants for MinValue and MaxValue is not likely to line up magically with whatever picture was
scribbled. So a mapping of scribble X0 to MinValue and Xn to MaxValue has to be made. There are two cases
to consider: There are fewer points in the latter than the former, and the compliment conditon.

Also, the returned values is from the weighted wheel of some newly computed length. So the two conversions
are sorted out here in dist_arb.c: 
      j = 0 ;
      for (i = 0 ; i < XlenFile; i++)
      {
        getStatsOnDistribution(1, &theValue, &ww_length, &XlenFile, &YminFile, &YmaxFile, "arbitrary_distribution_file.txt") ;
        scaledVal = (int) ((float)i * (float)(xmax-xmin)/(float)XlenFile) + xmin ;

        for (k=0; k < theValue ; k++)
        {
          if ((j+k) > ww_length) break ;
          X[j+k] = scaledVal ;
        }
        j = j + k ;
      }
where
  • i pulls from the original distribution length (1024 in my cases),
  • scaledVal manages the proportion of the former and latter, offset by xmin, and
  • j and k fill the array X, the weighted wheel, as described earlier.



Here's the code


The code for the testbench comprises the following:
arbitrary.sv
arbitrary_distribution_file.txt
dist_arb.c
tb_pkg.svh
The 'main.c' file here is just for testing in a C only environment:
main.c



Testing


I scribbled in two distributions and ran them with different ranges of MinVal and MaxVal.
I copied the output of the simulation from the write statements in arbitrary.sv into a file, b.csv
and generated a histogram with gnuplot like so: 
% more plotthis.dat 
clear ;
reset ;
set key off ;
set border 3 ;
# Each bar is half the (visual) width of its x-range.
set boxwidth 0.05 absolute ;
set style fill solid 1.0 noborder ;
bin_width = 0.1;
bin_number(x) = floor(x/bin_width) ;
rounded(x) = bin_width * ( bin_number(x) + 0.5 ) ;
plot 'b.csv' using (rounded($1)):(1) smooth frequency with boxes ;

% gnuplot -background white -persist plotthis.dat
The first arbitrary curve in gimp:


The first arbitrary curve after translation:


Simulation output of 4500 randomizations using MinVal=15 and MaxVal=110:



Note what happens with a simulation 4500 randomizations using a very different range of MinVal=64 and MaxVal=1500.
There are far fewer bins and the distribution has somewhat lost its look:


Here is the second arbitrary curve in gimp:


The second arbitrary curve after translation:


Simulation output of 4500 randomizations using MinVal=1 and MaxVal=100:




Problems


1) The code theData = X[rand() % ww_length] ; is a terrible way to generate random numbers.

2) Not just in the satement rand() % ww_length, but elsewhere as well I assume that ww_length is
less than the size of int. Even an average value of 50 in an array of length 1024 comes to a ww_length
of 51200 ... so I will need to fix that.

3) There is a potential for some severe binning going on. Using an input scribble of length of 1024
and a requested range of, say, 0 to 127, compresses, or bins, the distribution into only 8 regions.
That might not reflect the desired shape. It is less of a problem going the other way.


TODO


1) Replace the weighted wheel with a smaller data structure. It's intuitive the way it is, but the
actual length need only be as long as the number of entries in the file (again, 1024 in the cases above).

2) Fix problems 1 and 2 above.

3) I ought to add an option to the Perl script translator to output the data as an exponential. The
distribution does look like what was sketched, but the scribble was a communication of intent, and
that sketch may have intended to communicate "lots of these values" and "not many of those values"
in what may have had more of an exponential feel to it.



C'est tout.