Throw up your hands in the face of complexity and make a "gut feeling" decision.
- An MBA on call wouldn't hurt in this case.
When it is unacceptable to have no solution, when enumeration and mathematical analysis are not practical, and when a purely random technique would leave too many questions, a genetic algorithm may be the right technique.
Essential characteristics of a genetic algorithm
Like any algorithm, a genetic algorithm is a well-defined set of instructions for performing a task or solving a problem. The genetic algorithm method will try a number of potential solutions, grade them, choose among them, and use parts of the best of those solutions in the next iteration.To demonstrate, we first we need a problem to solve.
A problem to solve
Find the maximum value in an array of integers.The problem presented here is trivial and solvable by a number of techniques. But in order to solve it with a genetic algorithm the problem must be:
- expressed as a coding of a set of its parameters,
- and there must be a method for evaluating the expression(s) for different values of the code.
Find the array index of the array's maximum value.
The method for evaluating the expression (2) becomes simply returning the value of the array at that index. Given an array of length N, the range of potential solutions are now integer values from 0 to N-1.
That is almost a sufficient coding of the parameters (1), or rather parameter, since there is only one in this simple example. If we "try a number of potential solutions" by only randomly choosing integer indexes we are running a purely random scheme. We would like the GA to do some of the work, so we further decompose the integer index into smaller bits. If we actually use bits, then the problem can then be restated this way:
Find a collection of bits that when represented as an integer is the array index of the array's maximum value.
The problem is now stated in a form that a GA can be applied to directly. I will use that to present the essential components of a GA: Initial Population, Fitness Function, Reproduction Function, Mutation Function, and Termination Criteria.
Initial Population
| GAs begin with a "population" of "members", where each of the members consist of a complete coding of the problem's parameters. In this example, the population is M members consisting of log2(N) randomly selected bits (which, as an integer, form the index into the array). These N bits are the "genome". |
Fitness Function
|
Whatever the method is for evaluating the expression for different values of the code (genome), that method is applied here. The particular method for this example is simply returning the value of the array using the genome of each member as an integer index. The returned value is the fitness.
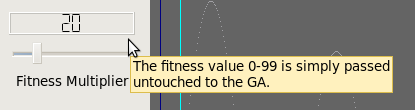
The complete "fitness function" could be more complex, such as applying a linear or exponential scaling of the returned value. It could include aspects the member's history such as a running average or the number of generations without changes to the genome. |
Reproduction Function
|
The M members will be graded by the fitness function. Some will be more "fit" than others. These are the members we are most interested in keeping and will feature in the reproduction (or "breeding" or "mating") process.
There are three primary steps to this reproduction, since we plan to wipe out all members' genomes and replace them with new genomes (new bits) each generation (iteration). The new members for the next iteration will be randomly selected from a pool of the old members, but the selection will be biased towards those most fit members. The steps are: 1. Create a "weighted roulette wheel", an array of values where each of the members is represented in proportion to thier fitness value. More fit members occupy more space in the array. This is done in a quite straight-forward way by populating an array with a number of member numbers, in proportion to thier fitness. This provides the bias towards the most fit. 2. Once the wheel is created a new generation is selected by choosing M random numbers from the weighted wheel. 3. But we won't just make copies when we repopulate the members' genomes. Since the members have been reduced to mere strings of bits, we can apply a "breeding" or "crossover" component. So the potential new members are paired for "mating", and sub-strings are swapped. Two 8-bit strings, for example, might take each others' lower 5 bits resulting in two completely new genomes (array indexes). |
Mutation Function
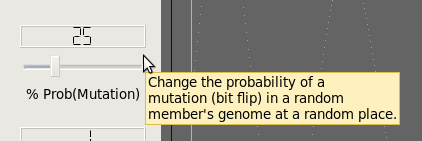
| Sometimes, things go wrong with the whole reproduction business. Occasionally one of the coded parameter values is copied incorrectly. At least we pretend it does. In this example all of those values are bits, so we "flip a bit" to mimic this loss of fidelity. |
Termination Criteria
|
Just like each of the M members in the initial population was evaluated, so too are the new "generation" of members evaluated. As generations go by the population diversity should shrink as the entire population converges towards representing the integer index of array returning the largest value. The decision of when to stop iterating and present a final population is what the "stopping" or "termination criteria" is about. Like other aspects of GAs, it is the subject of much research.
Common conditions for stopping are: |
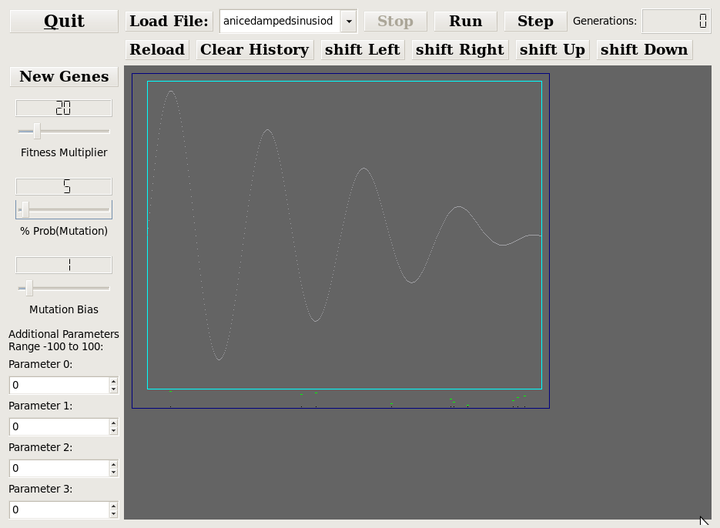
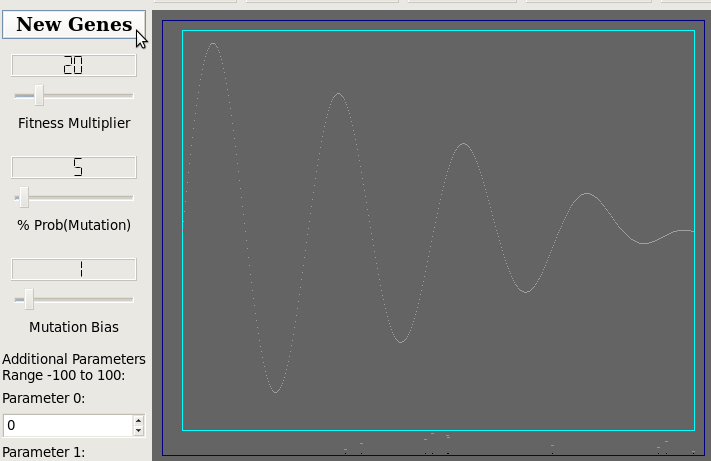
The Genetic Algorithm Demo
This section provides details of my specific implementation of the GA used to solve theFind the maximum value in an array of integers
problem, and screenshots of the Qt based GUI used to control and display the operation of the GA. The actual GA is named "gaga", because it's a "baby" GA.
(Sorry. I typed gaga.cpp and had no reason to change it).
In the sections below, Initial Population, Fitness Function, Reproduction Function, Mutation Function, and Termination Criteria, I will repeat the text from the previous section Essential characteristics of a genetic algorithm and those sections will be highlighted
like this text here is highlighted.The screenshot below provides notes for the discussion following.
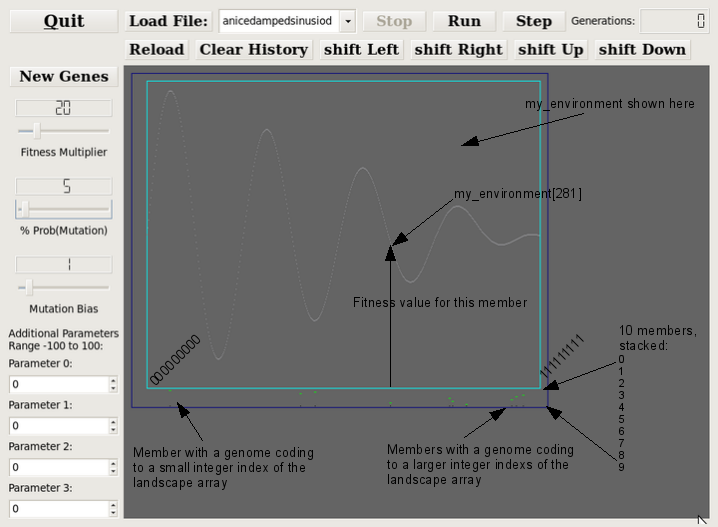
Initial Population
Fitness Function
Reproduction Function
The M members have been graded by the fitness function. Some are more "fit" than others. These are the members we are most interested in keeping and will feature in the reproduction (or "breeding" or "mating") process.This is how the weighted wheel is implemented in gaga:
ww = (int*) (malloc(total_fitness*sizeof(int))) ;
...
for (membr=0;membr<MEMBERS;membr++)
{
for (int fit=0;fit<fitness[membr];fit++)
{
ww[fitscan] = membr ;
fitscan++ ;
}
}
2. Once the wheel is created a new generation is selected by choosing M random numbers from the weighted wheel.
for (membr=0;membr<MEMBERS;membr++)
{
a_random_num = rand() % total_fitness ; // Choose some point in the total fitness.
breeding_units[membr] = ww[a_random_num] ;
}
3. But we won't just make copies when we repopulate the members' genomes. Since the members have been reduced to mere strings of bits, we can apply a "breeding" or "crossover" component. So the potential new members are paired for "mating", and sub-strings are swapped. Two 8-bit strings, for example, might take each others' lower 5 bits resulting in two completely new genomes (array indexes).
for (membr=0;membr<MEMBERS;membr++)
{
// Choose some point to cross/split gene
//
a_random_num = rand() % GENOME_BITS ;
copy_mmbr(my_mmbrsNew[membr], my_mmbrs[breeding_units[membr]]) ;
copy_mmbr(my_mmbrsNew[membr+1], my_mmbrs[breeding_units[membr+1]]) ;
for (int split = 0;split < a_random_num; split++)
{
my_mmbrsNew[membr][split] = my_mmbrs[breeding_units[membr+1]][split] ;
my_mmbrsNew[membr+1][split] = my_mmbrs[breeding_units[membr]][split] ;
}
membr++ ;
}
There is nothing to see here on the GUI with respect to this part of the GA except for the results. There are no run-time parameters to change the reproduction function. |
Mutation Function
Termination Criteria
Just like each of the M members in the initial population was evaluated, so too are the new "generation" of members evaluated. As generations go by the population diversity should shrink as the entire population converges towards representing the integer index of array returning the largest value. The decision of when to stop iterating and present a final population is what the "stopping" or "termination criteria" is about. Like other aspects of GAs, it is the subject of much research.There is no actual stopping criteria built into gaga. It will run and modify the population's genome and return. Any termination decision must be made elsewhere.
The collection of screenshot fragments below shows several successive clicks of the "Step" button. Each step resulted in a convergence of the 10 member's genomes towards the high point of the curve. The stopping criteria was simple: stop clicking the "Step" button when I've accumulated an illustrative set of screenshots. 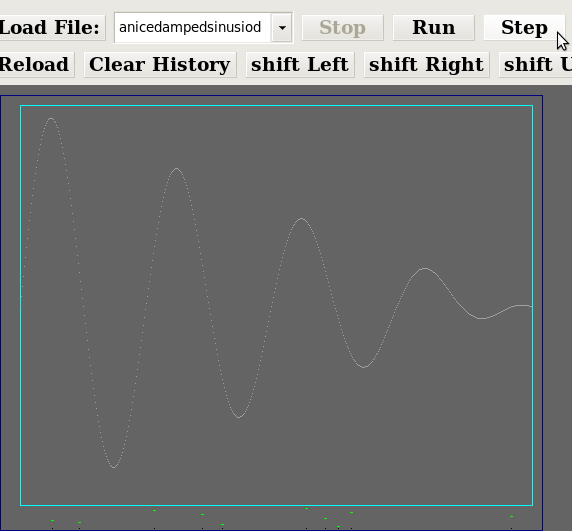 Step 1 Step 1 Step 2 Step 2 Step 3 Step 3 Step 4 Step 4 Step 5 Step 5 Step 6 Step 6 Step 15 Step 15 Step 17 Step 17 Step 18 Step 18
|
That ends the tour of the GA
gaga and the graphical interface for a nine-bit instance of gaga.