A UVM based Coercion Engine
Top of this page an outline brief elaboration implementation beginnings Something is missing
Other projects

The verification problems I am concerned with here are those cases where the interaction of independent and loosely-connected FSMs is rare ... rare and difficult to orchestrate with constrained random stimulus. I'll call this general condition M&Ms (FSM M1 in state Sm while FSM M2 is in state Sn).
Coverage data from constrained random sequences can tell you what got missed in simulation. Then targeted directed tests can be written to hit these cases after they have been identified. But we already know what the M&Ms are ... they are on our testplan after all. But they are likely on the testplan as higher level descriptions.
So how do we turn those high level descriptions into stimuli and hit those M&Ms automatically? This work is a preliminary investigation along that line.
Tools such as inFact™ from Mentor Graphics, the path tracing tool from nusym (since bought by Synopsys), and tools that perform automatic constraint extraction and run-time modification (see Coverage-directed test generation through automatic constraint extraction, Onur Guzey, Li-C. Wang) perform similar functions. But this is something you can do at home for free (because you write verification code at home for fun, don't you?)
It might soon be available, in part, on EDAplayground.

This is a work in progress

The Coercion Engine, in three passes




Pass one, outline

Considering only a single FSM, in order to coerce it into each state some things are needed. These are:
• A means to know what state a given FSM is in,
• Knowledge of what paths a given FSM can take,
• A means to track what paths a given FSM has already taken,
• A means to change the stimulus during runtime based on all of the above,
• A means to force a given FSM down a particular path.

Here is a reference diagram for the discussion below:



 
 
 

Pass two, brief elaboration

A means to know what state a given FSM is in

The testbench must have access to the state of the FSM in question. Either by backdoor access, or because it's an output from the DUT. If the FSM in question is built by FSMgen.pl (described elsewhere) then the job is done, the states are known, and it's all in a standard format.

Knowledge of what paths a given FSM can take

There first needs to be some description of the paths that can be taken. If the FSM in question is built by FSMgen.pl then the job is done and contained in a <name>_paths.txt file. More on that later.

A means to track what paths a given FSM has already taken

Given the description of the paths that can be taken, acceptor class automata can be used to provide this tracking information. The script Pathtracker.pl currently builds those automata as RTL. (SystemVerilog behavioral style models and scoreboard matrices are on the way.) These automata reside in the pathtracker block, track the FSM state, and tell the accountant block what paths have been taken and what is outstanding ... including all possible next states.

A means to change the stimulus during runtime based on all of the above

The accountant block only does the re-weighting and pressures the coercer block accordingly.

A means to force a given FSM down a particular path

Based on the accountant's biases, the coercer block just grabs sequences from a "bank" or "library".

 
 
 

Pass three, beginnings of an implementation

A means to know what state a given FSM is in,
Knowledge of what paths a given FSM can take,
A means to track what paths a given FSM has already taken


For the three items above, the pair of scripts FSMgen.pl and Pathmaker.pl provide the data.
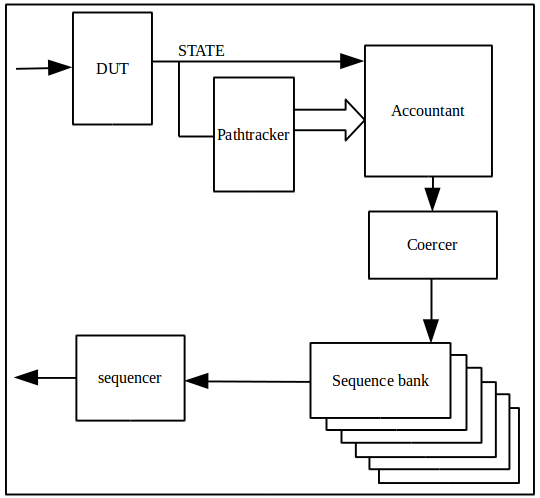
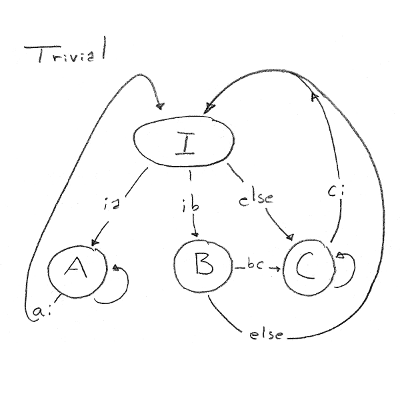
Consider the trivial state machine described and pictured to the right. The Verilog RTL produced by FSMgen.pl (below the bubble diagram) has STATE as a primary output. The path information produced by FSMgen.pl is as follows (from trivial_paths.txt): 
BITS=2 
CLK=clk  
RESET=reset
STATE :: I : 00
STATE :: A : 01
STATE :: B : 10
STATE :: C : 11
path1:I(ia)A(ai)I
path2:I(ib)B(ELSE)I
path3:I(ELSE)C(ci)I
path4:I(ia)A+(ai)I
path5:I(ib)B(bc)C(ci)I
path6:I(ELSE)C+(ci)I
path7:I(ib)B(bc)C+(ci)I

Using trivial_paths.txt as an input, the script Pathmaker.pl produces one acceptor automata per path. Here is the acceptor automata for path7: 
//Path path7 is I(ib)B(bc)C+(ci)I
module path7 (
  input [1:0]STATE,
  input clk,
  input reset,
  output [4:0]EXPECTING,
  output ok2spin,
  output doing,
  output done) ;

  logic [3:0] FSM ;
  logic [3:0] nextstate ;
  logic doing ;
  logic done ;
  localparam I = 2'b00 ;
  localparam A = 2'b01 ;
  localparam B = 2'b10 ;
  localparam C = 2'b11 ;

  localparam my_ZERO = 4'd0 ;
  localparam my_I    = 4'd1 ;
  localparam my_B    = 4'd2 ;
  localparam my_C    = 4'd4 ;
  localparam my_DONE = 4'd8 ;

  assign doing = |FSM ;
  assign done  =  FSM[3] ;

  always_comb
    begin
      if      (STATE == I) EXPECTING = B ;
      else if (STATE == B) EXPECTING = C ;
      else if (STATE == C) EXPECTING = I ;
   end

  // Registered part of the FSM:
  always @(posedge clk or posedge reset)
  begin
    if   (reset) FSM <= my_ZERO ;
    else         FSM <= nextstate ;
  end

  // Combinatorial part of the FSM:
  always_comb
  begin
    nextstate = 'bx ;
    case (FSM)
      my_ZERO : if (STATE == I)      nextstate = my_I ;
                else                 nextstate = my_ZERO ;

      my_I :    if      (STATE == B) nextstate = my_B ;
                else if (STATE == I) nextstate = my_I ;
                else                 nextstate = my_ZERO ;

      my_B :    if (STATE == C)      nextstate = my_C ;
                else                 nextstate = my_ZERO ;

      my_C :    if (STATE == I)      nextstate = my_DONE ;
                else                 nextstate = my_C ;

      my_DONE :                      nextstate = my_DONE ;

    endcase
  end

  //And a final output
  assign ok2spin =  (FSM == C) ;

endmodule


trivial.fsm

NAME=trivial
CLK = clk
RESET = reset
ENCODING = BINARY

INITIALSTATE = I
IDLESTATE = I

I(ia)A
I(ib)B
I(ELSE)C

A(ai)I
B(bc)C
B(ELSE)I
C(ci)I

bored <= I
busy1 <= A
busy2 <= C


module trivial (
  input  clk,
  input  reset,
  input  ia,
  input  ib,
  input  ai,
  input  bc,
  input  ci,
  output bored,
  output busy2,
  output busy1,
  output [1:0] STATE) ;

  localparam I = 2'b00 ;
  localparam A = 2'b01 ;
  localparam B = 2'b10 ;
  localparam C = 2'b11 ;

  // State driven outputs:
  assign bored =  (STATE == I)  ;
  assign busy2 =  (STATE == C)  ;
  assign busy1 =  (STATE == A)  ;

  // Register part of the FSM
  logic [1:0] STATE, nextstate ;

  always @(posedge clk or posedge reset) 
  begin
    if   ( reset ) STATE <= I ;
    else           STATE <= nextstate ;
  end

  // Combinatorial part of the FSM:
  always_comb
  begin
    nextstate = 'bx ;
    case (STATE)
      I : if      (ia) nextstate = A ;
          else if (ib) nextstate = B ;
          else         nextstate = C ;
      A : if      (ai) nextstate = I ;
          else         nextstate = A ;
      B : if      (bc) nextstate = C ;
          else         nextstate = I ;
      C : if      (ci) nextstate = I ;
          else         nextstate = C ;
    endcase
  end
endmodule

A means to change the stimulus during runtime based on all of the above

The Pathtracker block contains all the acceptor automata and provides the accountant block with both a list of outstanding paths (those not asserting "done") and the expected next state. The accountant performs re-weighting and passes that bias plus the expected next state on to the coercer block. As an example of the account in action, refer to the diagram above and count the number of possible paths.
With the weights based on how many possibilities exist down each path (and from each state), initially the weights to go from state I are:
I to A, 2/7,
I to B, 3/7, and
I to C 2/7
respectively. In a SystemVerilog dist, that's IA:=2, IB:=3, IC:=2.
If path 1 is later found to be taken, the path1 automata is asserting "done", the total number of paths remaining is 6, and the weights change to 1/6, 3/6, and 2/6 (or IA:=1, IB:=3, IC:=2). So the weights now favor the other paths more. Not too much more, but that's what comes from a trivial state machine. Keeping each possible path with a minimum of 1 keeps that path in the constrained random loop.

A means to force a given FSM down a particular path

The coercer block just grabs sequences based on the accountant's biases. One of the ways to do this is shown in the code to the right ... SystemVerilog allows dist weights to be variables. One would want to replace the case and $display with randsequence and sequences of course. The code shows how the original weights change from 2, 5, and 10 to 1, 1, and 1. 
Weights are  2, 5, 10
In 2 with W2           5
In 2 with W2           4
In 3 with W2          10
In 3 with W2           9
In 1 with W1           2
In 2 with W2           3
In 1 with W1           1
In 3 with W2           8
In 2 with W2           2
In 3 with W2           7
In 2 with W2           1
In 2 with W2           1
In 1 with W1           1
In 3 with W2           6
In 2 with W2           1
In 1 with W1           1
In 3 with W2           5
In 3 with W2           4
In 3 with W2           3
In 3 with W2           2
In 3 with W2           1
In 3 with W2           1
In 1 with W1           1
In 3 with W2           1
In 3 with W2           1
In 1 with W1           1
In 2 with W2           1
In 1 with W1           1
In 3 with W2           1
In 3 with W2           1

class Weights ;
  int W1, W2, W3 ;
  rand bit [1:0] t ;
  constraint aconstraint {t dist {1:=W1, 2:=W2, 3:= W3} ;}

  function set (int i, int j, int k) ;
    W1 = i ; W2 = j ; W3 = k ;
  endfunction

endclass

program DynamicWeightChanger;
  integer W1, W2, W3 ;

  Weights wts ;

  initial
  begin
    W1 =  2 ;
    W2 =  5 ;
    W3 = 10 ;

    wts = new ;

    $display ("Weights are %d, %d, %d", W1, W2, W3);

    repeat (30) begin
      wts.set(W1, W2, W3);
      wts.randomize() ;
      case (wts.t)
        1 : begin $display ("In 1 with W1 %d", W1) ; if (W1 > 1) W1-- ; end 
        2 : begin $display ("In 2 with W2 %d", W2) ; if (W2 > 1) W2-- ; end 
        3 : begin $display ("In 3 with W2 %d", W3) ; if (W3 > 1) W3-- ; end 
      endcase
    end
  end

endprogram



 
 
 

Something is missing

This is a preliminary write-up. It's all about the stimulus required to orchestrate simultaneous macro level events in different parts of the system, and that has not been addressed. What I'm after is creating the framework for calling in stimulus from a set of stimuli expected to cause a particular state to obtain, and choosing among them at runtime. The stimulus can be a fragment of assembly or C, a primitive transactions, or a longer sequence. That shouldn't matter. What should matter is what it does, at the "how we talk about it" level. For example, you may want to cause a translation fault. Now there are lots of ways to cause different kinds of translations faults. So there should be a mechanism that simply asks for a sequence that causes a translation fault. Someone needs to build these sequence libraries of course, but once they are there, and if they are built with the right concerns in mind, we can raise the level of abstraction for verification. SystemVerilog and the whole UVM thing is a language and method to do verification with, but it's not a Verification Language. There's too much typing involved and no good way to capture higher level concerns as low level stimuli.

Maybe I'll have to create a real High Level Verification Language. Something from Domain Specific Modeling perhaps. Hmmm ... thoughts are forming now ... and I think I've just need to tag this onto Graph Based Testing and what Accellera is doing with the Portable Stimulus - Working Group, PS-WG.

NOTE: Why, one might ask, all the fuss with the automata and pathtracker and accountant? First, one of the intentions was to have this run in emulation, so having as much of this as possible in RTL was a goal. Second, SystemVerilog does allow cover bins to specify a set of transitions, but I believe runtime bin data is not available for reading at present.
Besides those, and even though one could write properties with SystemVerilog assertions to check for, well, whatever you can imagine, the data for those transition bins and assertions has to come from somewhere. I recommend generating them from source using something like the FSMgen.pl and Pathmaker.pl scripts.
This is a work in progress